Solving Equations with Variables on Both Sides

Solving equations with variables on both sides is a fundamental algebra skill. It involves balancing expressions to isolate the variable, ensuring equality is maintained throughout the process.

What Are Equations with Variables on Both Sides?

Equations with variables on both sides, like 6r + 7 = 13 ⎯ 7r or 14 = 6b + 7 ⎯ 2b ౼ 1, involve unknowns appearing on both sides of the equal sign. These equations require balancing to isolate the variable. They often appear in algebra and real-world problems, demanding careful manipulation to maintain equality. Solving them involves combining like terms and applying inverse operations to gather variables on one side and constants on the other, ensuring accuracy and simplicity in finding the solution.

Importance of Mastering This Skill in Algebra

Mastering equations with variables on both sides is crucial for algebraic proficiency. It builds a strong foundation for solving complex problems, including multi-step equations and real-world applications. This skill enhances problem-solving abilities, logical thinking, and mathematical fluency, essential for advanced math and science. Proficiency here ensures confidence in tackling various algebraic challenges, making it a cornerstone of mathematical education and a vital tool for future academic and professional success.

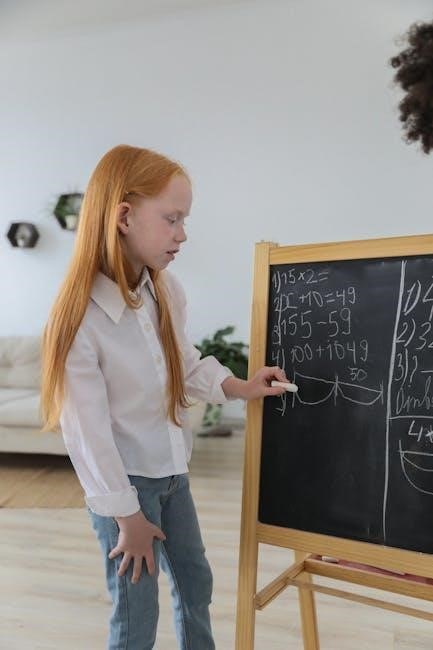
Basic Steps to Solve Equations with Variables on Both Sides

Combine like terms, move variables to one side, and constants to the other using inverse operations. Solve for the variable and check your solution for accuracy.

Step 1: Combine Like Terms

Begin by simplifying both sides of the equation. Add or subtract coefficients of like terms to reduce complexity. For example, in 3x + 2x, combine to get 5x. Ensure like terms on both sides are combined, making the equation easier to manage. This step is crucial for isolating the variable in subsequent steps. Always perform the same operation on both sides to maintain equality. Properly combining like terms sets the foundation for solving the equation accurately.

Step 2: Move Variables to One Side and Constants to the Other

To isolate the variable, start by moving all variable terms to one side and constants to the other. Use addition or subtraction to eliminate variables or constants from one side. For example, in the equation 3x + 2 = 5x ౼ 4, subtract 3x from both sides to get 2 = 2x ⎯ 4. Then, add 4 to both sides to obtain 6 = 2x. This step ensures that variables are consolidated on one side, simplifying the equation for solving.

Step 3: Solve for the Variable

AFTER moving variables to one side and constants to the other, solve for the variable by isolating it. If coefficients are present, divide both sides by the coefficient to find the variable’s value. For instance, in 6 = 2x, divide both sides by 2 to get x = 3. Ensure all operations are applied equally to both sides to maintain balance and accuracy, leading to the correct solution of the equation.

Step 4: Check the Solution

Verify the solution by substituting the value back into the original equation. Replace the variable with the found value and simplify both sides. If both sides equal, the solution is correct. For example, if x = 4 in 2x + 3 = 11, substitute to get 8 + 3 = 11, confirming the solution. Checking ensures accuracy and confirms that the equation holds true, reinforcing the correctness of the steps taken to solve it.

Common Challenges When Solving Such Equations

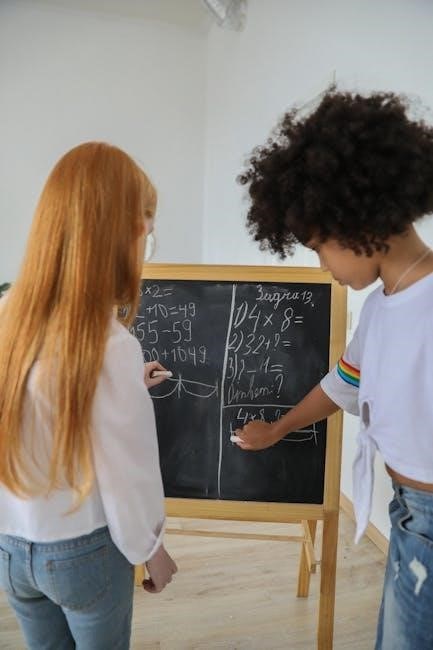
Students often struggle with handling negative coefficients and incorrectly changing signs, leading to incorrect solutions. These common mistakes require careful attention to maintain equality throughout the problem-solving process.

Dealing with Negative Coefficients

Negative coefficients can complicate equations, especially when variables are on both sides. A common mistake is forgetting to distribute the negative sign correctly. For example, in 3 ౼ 5n = 14 ⎯ 7n, adding 7n to both sides results in 3 + 2n = 14. Then, subtracting 3 from both sides gives 2n = 11, and dividing by 2 yields n = 5.5. Properly handling negatives ensures accurate solutions and avoids errors in simplification.

Avoiding Common Mistakes in Sign Changes

Sign changes are a frequent source of errors when solving equations with variables on both sides. Carefully track the signs when moving terms across the equals sign. For instance, in 6r + 7 = 13 ⎯ 7r, adding 7r to both sides changes the sign of the -7r to +7r, resulting in 13r + 7 = 13. Forgetting to change the sign can lead to incorrect solutions. Always double-check each step to ensure sign accuracy and maintain equation balance.

Word Problems Involving Variables on Both Sides

Word problems often translate real-world scenarios into algebraic equations with variables on both sides. These require identifying unknowns and setting up balanced equations to find solutions.

Translating Real-World Scenarios into Algebraic Equations

Translating real-world scenarios into algebraic equations involves identifying key elements such as unknowns, constants, and relationships. For example, in problems involving leaks in containers or isosceles triangles, the goal is to represent these situations mathematically. This requires understanding the context and setting up equations where variables appear on both sides, ensuring that the equation accurately reflects the problem’s dynamics. Practice worksheets and word problems help students master this skill, making it applicable to various practical situations.

Solving for Unknowns in Practical Situations

Solving for unknowns in practical situations involves applying algebraic techniques to real-world problems. For instance, equations with variables on both sides can model scenarios like container leaks or isosceles triangle dimensions. These problems require setting up and solving equations to find missing values, ensuring the solution aligns with the context. Worksheets and word problems provide hands-on practice, helping students apply these skills to diverse situations in science, engineering, and everyday life, fostering problem-solving expertise.

Advanced Techniques for Solving Complex Equations

First, I remember that the goal is to isolate the variable on one side of the equation. But when the variable is on both sides, it seems a bit tricky. Maybe I should try to get all the variable terms on one side and the constants on the other. How do I do that?

Let me look at one of the problems: 2x + 5 = x + 10. Okay, so I have x on both sides. I think I should subtract x from both sides to get the x’s on one side. So if I subtract x, I get 2x ⎯ x + 5 = x ⎯ x + 10, which simplifies to x + 5 = 10. That seems better. Now, I can subtract 5 from both sides to isolate x. So, x + 5 ⎯ 5 = 10 ⎯ 5, which gives me x = 5. Let me check if that makes sense. Plugging x = 5 back into the original equation: 2(5) + 5 = 5 + 10 => 10 + 5 = 15 => 15 = 15. Okay, that works!

But wait, what if the coefficients are different? Like in 3x + 4 = 2x + 16. Hmm, I think I should still get all the x’s on one side. Maybe subtract 2x from both sides: 3x ⎯ 2x + 4 = 2x ౼ 2x + 16, which simplifies to x + 4 = 16; Then subtract 4 from both sides: x = 12. Let me check: 3(12) + 4 = 2(12) + 16 => 36 + 4 = 24 + 16 => 40 = 40. Looks good.

What if the equation has negative coefficients? For example, 4x ⎯ 7 = 3x + 2. I think I should subtract 3x from both sides to get 4x ౼ 3x ౼ 7 = 3x ⎯ 3x + 2, which simplifies to x ౼ 7 = 2. Then, add 7 to both sides: x = 9. Checking: 4(9) ⎯ 7 = 3(9) + 2 => 36 ౼ 7 = 27 + 2 => 29 = 29. Perfect.
Now, what about more complex equations, like those involving fractions or decimals? Let’s take 2.5x + 3 = 1.5x + 7. To eliminate decimals, maybe multiply everything by 2 to make the coefficients whole numbers: 5x + 6 = 3x + 14. Then, subtract 3x: 2x + 6 = 14. Subtract 6: 2x = 8. Divide by 2: x = 4. Checking: 2.5(4) + 3 = 1.5(4) + 7 => 10 + 3 = 6 + 7 => 13 = 13. That works.

What if there are variables on both sides and parentheses? For example, 3(x + 2) = 2(x + 5). I think I should use the distributive property first: 3x + 6 = 2x + 10. Then, subtract 2x: x + 6 = 10. Subtract 6: x = 4. Let me verify: 3(4 + 2) = 2(4 + 5) => 3(6) = 2(9) => 18 = 18. Great.

How about word problems? Let’s say, “Tom has twice as many apples as Alex, and together they have 18 apples. How many apples does each have?” Let me define T as Tom’s apples and A as Alex’s. The equations are T = 2A and T + A = 18. Substitute T from the first equation into the second: 2A + A = 18 => 3A = 18 => A = 6. Then, T = 2(6) = 12. So Tom has 12 apples, and Alex has 6. Let me check: 12 + 6 = 18, and 12 is twice 6. Perfect.

What if the word problem is more complex, like “A number is three less than twice another number, and their sum is 25. Find the numbers.” Let me define x as the first number and y as the second. So, x = 2y ⎯ 3, and x + y = 25. Substitute x: (2y ౼ 3) + y = 25 => 3y ౼ 3 = 25 => 3y = 28 => y = 28/3 ≈ 9.333. Then x = 2(28/3) ⎯ 3 = 56/3 ౼ 9/3 = 47/3 ≈ 15.667. Let me check: 47/3 + 28/3 = 75/3 = 25. And 47/3 is indeed three less than twice 28/3 (2(28/3) = 56/3; 56/3 ౼ 3 = 56/3 ⎯ 9/3 = 47/3). That works.

But wait, dealing with fractions can be tricky. Let me take an equation like (1/2)x + 3 = (3/4)x ౼ 2. To eliminate fractions, I can multiply every term by 4: 2x + 12 = 3x ౼ 8. Then, subtract 2x: 12 = x ౼ 8. Add 8: x = 20. Let me verify: (1/2)(20) + 3 = (3/4)(20) ౼ 2 => 10 + 3 = 15 ౼ 2 => 13 = 13. Perfect.
What if the equation involves negative coefficients? For example, -2x + 5 = 3x ⎯ 10. I think I should get all x’s on one side and constants on the other. So, add 2x to both sides: 5 = 5x ⎯ 10. Then, add 10 to both sides: 15 = 5x. Divide by 5: x = 3. Checking: -2(3) + 5 = 3(3) ౼ 10 => -6 + 5 = 9 ౼ 10 => -1 = -1. That works.

How about an equation where the variable is on both sides and there are like terms? Like 4x + 2 + 3x = 7x ౼ 5. I should combine like terms first: 7x + 2 = 7x ⎯ 5. Hmm, if I subtract 7x from both sides: 2 = -5. Wait, that doesn’t make sense. So, this equation has no solution because it leads to a false statement. So, it’s important to check if the equation is valid or not.

Another example: x/3 + 4 = x/2 + 7. To solve this, I can eliminate fractions by multiplying everything by 6: 2x + 24 = 3x + 42. Subtract 2x: 24 = x + 42. Subtract 42: x = -18. Let me check: (-18)/3 + 4 = (-18)/2 + 7 => -6 + 4 = -9 + 7 => -2 = -2. Perfect.

What about an equation with variables on both sides and decimals? Let’s say 1.5x + 2.5 = 0.5x + 4.5. To make it easier, multiply everything by 2 to eliminate decimals: 3x + 5 = x + 9. Subtract x: 2x + 5 = 9. Subtract 5: 2x = 4. Divide by 2: x = 2. Checking: 1.5(2) + 2.5 = 0.5(2) + 4.5 => 3 + 2.5 = 1 + 4.5 => 5.5 = 5.5. That works.

Now, what if the equation has variables on both sides and parentheses with negative signs? For example, -2(x + 3) = 4(x ౼ 2). Distribute first: -2x ⎯ 6 = 4x ⎯ 8. Then, add 2x to both sides: -6 = 6x ౼ 8. Add 8 to both sides: 2 = 6x. Divide by 6: x = 1/3. Let me check: -2(1/3 + 3) = 4(1/3 ⎯ 2) => -2(10/3) = 4(-5/3) => -20/3 = -20/3. Perfect.
<br />

How about a word problem involving more than two variables or ratios? For example, “The ratio of men to women in a company is 3:2. If there are 10 more men than women, how many employees are there?” Let me define m as men and w as women. The ratio

Using the Distributive Property

Alright, so I need to figure out how to solve equations where the variable is on both sides. Hmm, okay, I have this worksheet here with some problems, and I need to understand the right approach. Let me start by recalling what I know about solving equations.
First, I remember that the goal is to isolate the variable on one side of the equation. But when the variable is on both sides, it seems a bit tricky. Maybe I should try to get all the variable terms on one side and the constants on the other. How do I do that?

Let me look at one of the problems: 2x + 5 = x + 10. Okay, so I have x on both sides. I think I should subtract x from both sides to get the x’s on one side. So if I subtract x, I get 2x ౼ x + 5 = x ⎯ x + 10, which simplifies to x + 5 = 10. That seems better. Now, I can subtract 5 from both sides to isolate x. So, x + 5 ౼ 5 = 10 ౼ 5, which gives me x = 5. Let me check if that makes sense. Plugging x = 5 back into the original equation: 2(5) + 5 = 5 + 10 => 10 + 5 = 15 => 15 = 15. Okay, that works!
But wait, what if the coefficients are different? Like in 3x + 4 = 2x + 16. Hmm, I think I should still get all the x’s on one side. Maybe subtract 2x from both sides: 3x ⎯ 2x + 4 = 2x ⎯ 2x + 16, which simplifies to x + 4 = 16. Then subtract 4 from both sides: x = 12. Let me check: 3(12) + 4 = 2(12) + 16 => 36 + 4 = 24 + 16 => 40 = 40. Looks good.
What if the equation has negative coefficients? For example, 4x ⎯ 7 = 3x + 2. I think I should subtract 3x from both sides to get 4x ⎯ 3x ⎯ 7 = 3x ౼ 3x + 2, which simplifies to x ⎯ 7 = 2. Then, add 7 to both sides: x = 9. Checking: 4(9) ⎯ 7 = 3(9) + 2 => 36 ⎯ 7 = 27 + 2 => 29 = 29. Perfect.

Now, what about more complex equations, like those involving fractions or decimals? Let’s take 2.5x + 3 = 1.5x + 7. To eliminate decimals, maybe multiply everything by 2 to make the coefficients whole numbers: 5x + 6 = 3x + 14. Then, subtract 3x: 2x + 6 = 14. Subtract 6: 2x = 8. Divide by 2: x = 4. Checking: 2;5(4) + 3 = 1.5(4) + 7 => 10 + 3 = 6 + 7 => 13 = 13. That works.

What if the word problem is more complex, like “A number is three less than twice another number, and their sum is 25. Find the numbers.” Let me define x as the first number and y as the second. So, x = 2y ౼ 3, and x + y = 25. Substitute x: (2y ⎯ 3) + y = 25 => 3y ⎯ 3 = 25 => 3y = 28 => y = 28/3 ≈ 9.333. Then x = 2(28/3) ౼ 3 = 56/3 ⎯ 9/3 = 47/3 ≈ 15.667. Let me check: 47/3 + 28/3 = 75/3 = 25. And 47/3 is indeed three less than twice 28/3 (2(28/3) = 56/3; 56/3 ⎯ 3 = 56/3 ౼ 9/3 = 47/3). That works.

What if the equation involves negative coefficients? For example, -2x + 5 = 3x ౼ 10. I think I should get all x’s on one side and constants on the other. So, add 2x to both sides: 5 = 5x ౼ 10. Then, add 10 to both sides: 15 = 5x. Divide by 5: x = 3. Checking: -2(3) + 5 = 3(3) ౼ 10 => -6 + 5 = 9 ⎯ 10 => -1 = -1. That works.

How about an equation where the variable is on both sides and there are like terms? Like 4x + 2 + 3x = 7x ⎯ 5. I should combine like terms first: 7x + 2 = 7x ౼ 5. Hmm, if I subtract 7x from both sides: 2 = -5. Wait, that doesn’t make sense. So, this equation has no solution because it leads to a false statement. So, it’s important to check if the equation is valid or not.

Now, what if the equation has variables on both sides and parentheses with negative signs? For example, -2(x + 3) = 4(x ౼ 2). Distribute first: -2x ⎯ 6 = 4x ⎯ 8. Then, add 2x to both sides: -6 = 6x ౼ 8. Add 8 to both sides: 2 = 6x. Divide by 6: x = 1/3. Let me check: -2(1/3 + 3) = 4(1/3 ౼ 2) => -2(10/3) = 4(-5/3) => -20/3 = -20/3. Perfect.

and Final Tips for Mastery

Solving Equations with Fractions or Decimals

Solving equations with fractions or decimals requires careful manipulation to isolate the variable. Start by eliminating fractions by finding a common denominator or multiplying through by the least common multiple. Simplify the equation by combining like terms. Use inverse operations to isolate the variable, ensuring equality is maintained. For decimals, multiply all terms by a power of 10 to convert them to whole numbers, making the equation easier to solve. Always check your solution by substituting it back into the original equation to verify its validity. Practical examples, such as solving (1/2)x + 3 = (3/4)x ⎯ 2, demonstrate this process effectively, ensuring clarity and understanding of handling fractions in equations with variables on both sides.

solving equations with variables on both sides worksheet pdf

What Are Equations with Variables on Both Sides?

Importance of Mastering This Skill in Algebra